5 erros comuns em regressão

Os modelos de regressão são bastante utilizados quando queremos estudar a relação entre uma variável resposta e várias variáveis independentes e quantificar seus efeitos. Porém, alguns cuidados devem ser tomados ao executar o ajuste para não prejudicar o seu trabalho. Erros comuns em regressão passam facilmente despercebidos, pois o software continuará calculando a regressão, podendo levar a decisões erradas e prejudicar todo o seu trabalho. Por isso separamos os 5 erros comuns em regressão e como evitá-los.

1) Quanto mais variáveis, melhor

• Erro: Um dos erros comuns em regressão, é achar que quanto mais variáveis independentes eu tiver para explicar a variável de interesse, melhor. Por exemplo, minha variável de interesse é a altura de uma pessoa e coleto dados de diversas variáveis como peso, idade, sexo, escolaridade, frequência cardíaca, cor do cabelo, etc.
• Consequência: Dificulta muito a interpretação do modelo. Quando ajustamos um modelo de regressão queremos que ele seja facilmente entendido. Imagina ter que explicar o efeito de cada variável independente na variável resposta? Além disso, algumas variáveis podem possuir um efeito baixíssimo e não serem relevantes para explicar a variável resposta.
• Solução: Antes de encher seu modelo de variáveis, observe as que você tem disponível e tente selecionar algumas poucas que você julgar serem relevantes para explicar a variável resposta. Depois de ajustada, verifique se a regressão é satisfatória. Se não for, daí sim tente acrescentar mas variáveis aos poucos.

2) Quanto maior a correlação entre as variáveis, melhor!

• Erro: Achar que quanto maior a correlação entre todas as variáveis (independentes e resposta), melhor será o ajuste.
• Consequência: Matematicamente, correlações altas entre as variáveis independentes causam uma instabilidade numérica ao ajustar a curva de regressão, o chamado efeito de multicolinearidade. Em outras palavras, redundância.
• Solução: Não confunda relação com correlação. É muito importante que as variáveis tenham alguma relação entre si para que você consiga explicar a regressão, mas valores altíssimos de correlação geram redundância e podem ser matematicamente prejudiciais. Uma dica é antes de ajustar o modelo de regressão verificar a correlação entre todas as variáveis independentes. Se existir uma correlação muito próxima de 1 ou -1 entre variáveis, escolha apenas uma delas para entrar no modelo.

3) R^2 é suficiente para avaliar minha regressão

• Erro: Depois de ajustado o modelo de regressão, achar que olhar apenas para o R^2 lhe dará informações suficientes para julgar se tem uma boa regressão ou não.
• Consequência: Podemos obter péssimas regressões com R^2 altíssimos. Matematicamente, o R^2 é uma proporção entre 0 e 1 que lhe diz o quanto da variabilidade da variável resposta pode ser explicada pela regressão. Porém, é um número que cresce sempre que adicionamos uma variável independente no modelo. Então, como vimos em 1), modelos com muitas variáveis nem sempre são bons modelos e terão R^2 altos. Um exemplo clássico de como podemos superestimar o poder de R^2 é o quarteto de Anscombe. Na figura abaixo temos quatro conjuntos de dados totalmente diferentes, mas de exatamente mesma regressão linear simples e R^2 de 0,816, valor considerado alto.
  
• Solução: A boa e velha solução é fazer o gráfico. Verifique como a regressão se ajusta em seus dados. Essa é a principal ferramenta para avaliar se seu ajuste foi bom ou não. O R^2 é útil quando queremos comparar dois modelos para o mesmo problema.

4) Dados tem que ser normais

• Erro: O pressuposto para ajustar uma regressão é que os dados sejam normais.
• Consequência: Você pode perder tempo tentando normalizar os dados, sendo que não há necessidade nenhuma para isso.
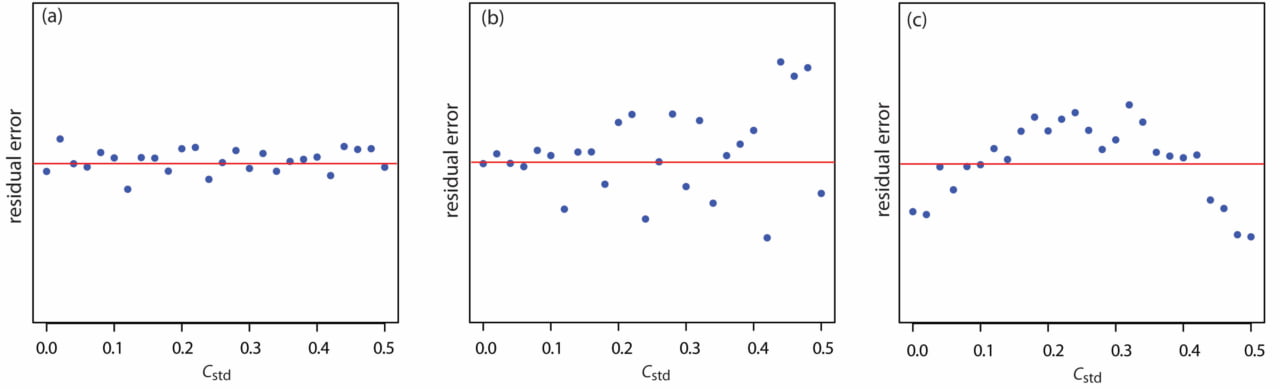
• Solução: O pressuposto principal é que os dados sejam contínuos e os resíduos (ou erros) tenham variância constante e sejam independentes. Ou seja, depois de ajustar a regressão faça um gráfico de dispersão dos resíduos (valor ajustado menos valor real) e veja se eles se concentram em torno do zero e tem uma variabilidade constante. Na imagem abaixo temos três gráficos de dispersão de resíduos para modelos diferentes. Na primeira figura os resíduos se concentram em torno do zero e possuem uma variabilidade aparentemente constante. Na segunda figura, os dados também se concentram em torno de zero, mas aparentemente a variabilidade aumenta no lado direito do gráfico. Por fim, na terceira figura temos dados não concentrados em torno de zero, mas variabilidade constante. Resumindo, apenas a primeira figura satisfaz os pressupostos do modelo.

5) Se a variável não for significativa, eu retiro da regressão. Sempre!

• Erro: Achar que ao fazer o teste de hipótese para verificar se a variável independente é significativa ou não é crucial para decidir se ela continua no modelo.
• Consequência: Você pode estar retirando uma variável muito importante para explicar sua variável resposta, mesmo que ela tenha se mostrado não significativa.
• Solução: Pare e pense além dos números e verifique qual a relação entre a variável independente e a variável resposta. Se antes de ajustar a regressão você tinha certeza absoluta de que aquela é a variável chave do modelo, pode ser que ela ainda seja, mas tenha um efeito pequeno. Afinal, o teste de hipótese verifica se o efeito é zero ou não e efeitos observados próximos de zero podem acusar não significância.

Vamos colocar em prática?

Agora você já sabe que erros não cometer ao ajustar um modelo de regressão. Só falta colocar na prática! Confira no botão abaixo mais 5 passos para fazer uma regressão show de bola, mas não se esqueça de verificar os 5 itens acima! Se deseja conhecer todos os segredos para construir e interpretar uma regressão, conheça o curso de Regressão Linear da Escola EDTI.