Estatística descritiva: o que é, objetivos, conceitos e quando usar

A estatística descritiva pode ser explicada como o ordenamento dos dados quando eles são aparentemente caóticos.

É um ramo fundamental para desenvolver o conhecimento, servindo como suporte para a compreensão de fenômenos sociais, biológicos, químicos e físicos, entre muitos outros.

Sem estatística descritiva, seria impossível fazer ciência, pelo menos não nos termos como se faz hoje.

Esse ramo não se aplica apenas aos laboratórios e experimentos acadêmicos.

Na prática, a estatística descritiva é amplamente usada para orientar gestores de empresas em suas decisões.

Na indústria, por exemplo, ela é um verdadeiro ponto de apoio nos processos de melhoria contínua e de detecção de falhas e problemas.

Por essa razão, líderes que têm a habilidade de trabalhar com dados tratados estatisticamente são muito mais requisitados no mercado.

Você pode ser um deles, começando por ler esse texto em que explicamos como funciona a parte descritiva da estatística e muito mais.

O que é estatística descritiva?

Estatística descritiva é a parte da ciência estatística na qual um conjunto de dados é organizado e padronizado para ser explicado de forma prática.

De certa forma, o objetivo final da estatística descritiva é resumir dados quando eles carecem de um ordenamento, de modo que permitam compreender um certo fenômeno.

Um bom exemplo disso está nos censos populacionais.

A cada censo, o IBGE levanta dados demográficos sobre a população brasileira que, quando cruzados com dados gerados pela Receita Federal, ajudam a entender certos fatos socioeconômicos.

Outro exemplo simples de aplicação da estatística descritiva está nas pesquisas de mercado que as empresas fazem para identificar o perfil dos seus clientes.

Elas podem, nesse caso, identificar que a maioria desses clientes são mulheres de uma certa faixa etária, por exemplo.

A partir disso, seus líderes saberão para quem devem ser direcionados os esforços de marketing, assim como a estratégia de vendas.

Qual a diferença entre estatística descritiva e inferencial?

Você provavelmente já deve ter observado no período eleitoral que, quando uma pesquisa de intenção de voto é divulgada, sempre é informada a “margem de erro”.

Isso acontece porque, nesse tipo de pesquisa, utilizam-se cálculos e ferramentas da estatística inferencial para projetar a quantidade de votos que cada candidato deve receber.

Ela parte de uma fração da população, considerando que é impossível saber da opinião de todos os brasileiros.

Assim, na estatística inferencial, estamos tratando sempre de probabilidades, tomando como base dados extraídos de uma amostra.

Isso faz com que a estatística inferencial se diferencie da descritiva por utilizar comparações.

Já na estatística descritiva, normalmente trabalhamos com dados fechados, ou seja, que já pertencem a uma população completa como objeto de análise.

Dessa forma, é possível representar esses dados por meio de gráficos e tabelas, bem como calcular medidas típicas de grupos fechados, como média, mediana, moda e a frequência.

Quais são os objetivos da estatística descritiva?

A partir do que vimos, é justo concluir que um dos principais objetivos da estatística descritiva é a organização dos dados.

Dessa forma, é possível compreender e analisar as ocorrências que geraram esses dados, o que pode até ajudar a fazer previsões.

Afinal, ao organizar, podemos encontrar padrões que são úteis para antecipar os fenômenos aos quais se relacionam.

Na indústria, a estatística descritiva é amplamente utilizada como ferramenta de trabalho para melhorar a qualidade e evitar a falha.

Os dados coletados de uma linha de montagem podem revelar “segredos” que ajudam os gestores a tomar decisões mais assertivas.

Assim, a estatística descritiva é um caminho para orientar quanto ao que fazer, evitando a aleatoriedade na gestão de negócios.

Qual a diferença entre estatística descritiva e inferencial?

Você provavelmente já deve ter observado no período eleitoral que, quando uma pesquisa de intenção de voto é divulgada, sempre é informada a “margem de erro”.

Isso acontece porque, nesse tipo de pesquisa, utilizam-se cálculos e ferramentas da estatística inferencial para projetar a quantidade de votos que cada candidato deve receber

 Quando usar a estatística descritiva

Em momentos em que estamos diante de muitos dados, é necessário tornar essas informações manejáveis para então relacioná-los. 

A estatística descritiva é o instrumento que torna possível reduzir essas informações, no entanto ao utiliza-lo também ocorre uma defasagem de informações.

Este viés introduzido pela redução da informação a um único número pode ser minimizado pela utilização de várias medidas que nos permitam cruzar informação e contrapor outras leituras dos nossos dados resumidos.

Esta é uma das razões pelas quais os dados estatísticos que se apresentam em relatórios de investigação terem frequentemente duas ou mais medidas descritivas associadas.

Por exemplo, o valor da Média (medida de tendência central) é frequentemente apresentado em associação com o valor do Desvio Padrão (medida de dispersão).

As medidas da Estatística Descritiva são também a base para a Estatística Inferencial (aquela que relaciona os dados da nossa distribuição).

A Estatística Descritiva descreve a nossa amostra e a Estatística Inferencial permite-nos fazer extrapolações dos resultados obtidos na nossa amostra para a população.

Permite-nos tirar conclusões, fazer estimativas, previsões e generalizações sobre todo um conjunto de dados estudando apenas parte dele.

Como fazer estatística descritiva no Excel?

Uma das medidas de frequência usadas na estatística descritiva é o desvio padrão, que consiste na média da dispersão dos dados de uma amostra em relação à média geral.

Para conhecê-lo, é preciso antes fazer uma série de cálculos, a começar pela própria média dos dados.

Pois esses cálculos preliminares podem ser realizados automaticamente no Excel, dispensando o uso de calculadoras manuais.

Aliás, no Excel você encontra fórmulas para fazer todo tipo de cálculo estatístico, inclusive inferenciais.

Para simplificar, digamos que você queira inicialmente saber a média do peso de um grupo de 10 pessoas.

Para isso, basta inserir os dados em uma coluna e, na célula logo depois do último dado inserir a fórmula como aparece na imagem abaixo:

 

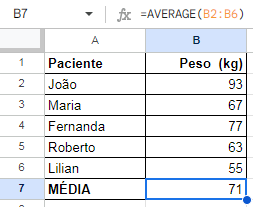
Exemplo de estatística descritiva

A propósito, o exemplo acima serve para ilustrar um uso bastante recorrente da estatística descritiva.

Pelo conjunto de dados que temos, poderíamos extrair outros dados para compreender melhor o objeto de estudo.

Podemos saber, por exemplo, o intervalo desses dados que, no caso, seria a diferença entre o maior e o menor peso.

Assim, temos: 93 – 55 = 38.

Com esses dados, podemos também calcular o desvio padrão, tarefa que fica muito mais simples quando utilizamos o Excel, como mostrado abaixo:

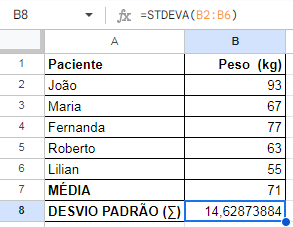
Imaginemos, então, que esses dados são sobre um experimento cujo objetivo seja comprovar que uma certa dieta ajuda a perder peso.

Nesse caso, pode ser interessante reduzir o intervalo dos dados, bem como o desvio padrão.

Esse mesmo princípio pode ser aplicado na indústria e em qualquer outra atividade que demanda algum tipo de controle sobre dados.

Conceitos da estatística descritiva

A estatística descritiva é uma ciência e, como tal, tem uma série de conceitos por trás para basear seus postulados, ainda que trabalhe fundamentalmente com números.

Eles servem como referência, de modo a dar sentido para os cálculos, ajudando a entender porque eles são feitos.

Confira a seguir.

Tratamento estatístico

O primeiro passo para o tratamento estatístico de dados é a sua organização numa base de dados.

A base de dados é uma tabela de dupla entrada em que habitualmente as colunas são usadas para colocar os dados referentes às variáveis e as linhas para identificar os sujeitos.

Na célula formada pela intercepção das linhas com as colunas coloca-se o valor da variável correspondente ao sujeito.  

A partir da informação organizada na nossa base de dados, podemos construir uma tabela de distribuição de frequências que nada mais é do que a identificação do número de vezes em que cada tipo de resposta ocorre.

Medidas de Tendência Central

Quando queremos resumir os dados de uma distribuição utilizando apenas um número recorremos a medidas de tendência central (Média, Moda e Mediana).  

A utilização destas três medidas varia conforme o tipo de informação que pretendemos resumir ou descrever.

Estatística descritiva: Percentis

Alguns percentis têm uma designação específica. Estas medidas permitem-nos situar os valores de cada observação em relação à distribuição total dos dados.

Uma vez que dividem o conjunto de observações em partes iguais tendo por referência o número de elementos que compõem a nossa amostra.

Elas são particularmente úteis quando queremos destacar um valor que marque um percentual de interesse. Também podem ser usadas para nos dar informação sobre o valor relativo de um dado valor numa distribuição.

Por exemplo, na análise das médias de estudantes com o mesmo curso feito em instituições diferentes, a mesma média situada em percentis diferentes, tem um valor relativo diferente.

Medidas de dispersão

O Desvio padrão é o valor que quantifica a dispersão das respostas numa distribuição normal, ou seja, a média das diferenças entre o valor de cada resposta e a média da distribuição (Nota: como a média da soma dos desvios é sempre igual a zero, elevam-se esses desvios ao quadrado e só depois é que se calcula a média desses desvios elevados ao quadrado, que se designa por Variância. Calculando a raiz quadrada da variância obtém-se o valor do desvio padrão).

O calculo da média dos desvios quadrados é feito dividindo a soma dos quadrados pelo valor de n-1  e não por n (a razão para este procedimento prende-se com o conceito de graus de liberdade).

Medidas de distribuição

O conceito de distribuição é fundamental na estatística. Toda a estatística paramétrica assenta no pressuposto de que os fatores e variáveis da população se distribuem de acordo com a distribuição normal.

Quando número de sujeitos ou de casos for suficientemente grande, a distribuição amostral da média se aproxima cada vez mais de uma distribuição normal.

A distribuição normal das variáveis em estudo é um pressuposto para a utilização de testes estatísticos paramétricos.

Quando os resultados não se distribuem de acordo com a curva normal, teremos de usar testes estatísticos não-paramétricos.

As medidas de dispersão permitem-nos avaliar se os nossos dados estão distribuídos de acordo com o padrão descrito acima, ou seja, verificar se temos uma distribuição normal, ou se há desvios nessa distribuição.

Para medir a distribuição usamos medidas de achatamento (Kurtose) ou de simetria e obliquidade da curva de distribuição (Skewness).

Conclusão

A estatística descritiva pode ser bastante estimulante, já que “ilumina” e explica dados, que passam a ser lidos e interpretados de outra forma.

Sem essa ramificação da estatística, jamais seríamos capazes de compreender fenômenos, orientar decisões e melhorar continuamente.

Você pode se tornar expert em estatística descritiva, formando-se como líder Green Belt ou Black Belt nos cursos da Escola EDTI.

Para saber ainda mais, acesse o e-book gratuito em que destacamos a importância da correlação entre variáveis para estabelecer relações de causa e efeito.