Os modelos probabilísticos são utilizados nas mais diversas áreas, eles simplificam a realidade dos dados ao mesmo tempo que apresentam suas principais características. Conhecendo a distribuição de probabilidade de uma variável aleatória é possível obter suas medidas de localização e de variação, como por exemplo, a média e a variância, aumentando o conhecimento sobre a variável de interesse e todo o processo.
Modelos probabilísticos para variáveis aleatórias discretas
Alguns modelos são muito utilizados quando falamos de variável aleatória discreta.
A Distribuição de Poisson é adequada para descrever situações onde existe uma probabilidade de ocorrência em um campo ou intervalo contínuo, geralmente tempo ou área. Por exemplo, o nº o de acidentes por mês, nº o de defeitos por metro quadrado, nº o de clientes atendidos por hora.
A Distribuição Binomial é utilizada para descrever situações em que a variável aleatória pode ser agrupada em apenas dois resultados possíveis, Sucesso ou Fracasso, os chamados ensaios de Bernoulli. Algumas propriedades desta distribuição são que a probabilidade de sucesso não muda de ensaio para ensaio e os ensaios são idênticos e independentes.
Exemplo: Suponha que numa linha de produção a probabilidade de se obter uma peça defeituosa é 
. Toma-se uma amostra de 10 peças para serem inspecionadas. Utilizando definições da distribuição Binominal podemos encontrar as respostas para as questões:
Qual a probabilidade de se obter uma peça defeituosa? Ou nenhuma peça defeituosa? Ou duas peças defeituosas?
Modelos probabilísticos para variáveis aleatórias contínuas.
A mais importante distribuição contínua de probabilidade é a Distribuição Normal ou Gaussiana. Muitas características contínuas tem distribuição razoavelmente simétrica e podem ser aproximadas por uma curva Normal. Alguns exemplos são alturas, pesos e outras características físicas, erros de medida em experimentos científicos, medidas de inteligência e aptidão, pontuações em testes variados e numerosas medidas e indicadores econômicos.
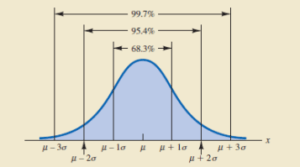
Todo gráfico da distribuição normal é simétrico em torno da média da distribuição e tem forma de sino, de modo que o centro do sino (ponto de simetria) é tanto a média como a mediana da distribuição. Uma propriedade importante da distribuição normal é devido à distribuição destes dados ser normal, você pode determinar exatamente que porcentagem dos valores caem em qualquer amplitude específica. Por exemplo: 68,3% dos valores estão a 1 desvio padrão da média, 95,4% dos valores estão a 2 desvios padrão da média e 99,7% dos valores estão a 3 desvios padrão da média.
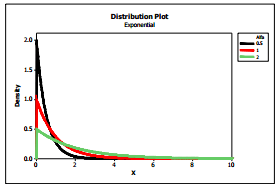
Outra distribuição para v.a. contínua é a Distribuição Exponencial, largamente utilizada em engenharia e em várias disciplinas da ciência. Este modelo ajusta-se bem a dados de tempo para ocorrência de um evento, por exemplo tempo para atendimento de uma chamada.
Relação entre a Poisson e a Exponencial
Existe uma importante relação entre esta e a distribuição de Poisson. Quando usamos a distribuição discreta de Poisson para modelar, por exemplo, o número de ligações em um intervalo de tempo é possível mostrar que o tempo entre duas ligações sucessivas terá distribuição exponencial.
Para saber mais sobre os modelos probabilísticos e como utilizá-los em projetos Seis Sigma confira nossos cursos de Black Belt, nas modalidades presenciais e EAD.