Você sabe o que é um Box plot? Provavelmente já ouviu falar e achou o nome desse gráfico estranho certo?
Na estatística, o Boxplot, ou diagrama de caixa, é uma maneira gráfica de representar a alteração dos dados de uma variável por meio de quartis.
Inicialmente desenvolvido por John W. Tukey, o box plot também é conhecido como box-and-whisker plot, diagrama de caixa, diagrama de extremos e quartis e tem a função parecida com um histograma.
Se você ficou curioso e quer saber mais sobre essa ferramenta, confira esse post que escrevemos para explicar como interpretar um box plot, quais conclusões tiramos ao analisar um boxplot, como preparar um gráfico box plot no excel, como preparar um no R e como o diagrama de caixa apresenta os outliers. Confira!
O que é um Box Plot
O Box Plot (também chamado de box e whisker plot) é um método alternativo ao histograma e ao ramo-e-folha para representar os dados.
O Box Plot fornece informação sobre as seguintes características do conjunto de dados: localização, dispersão, assimetria, comprimento da cauda e outliers (medidas discrepantes).
Embora o Boxplot forneça informação sobre localização e dispersão, seu verdadeiro valor está na informação que fornece sobre a cauda da distribuição.
Pontos desgarrados (Outliers) podem afetar de forma adversa as decisões a serem tomadas a partir da análise dos dados se não forem devidamente considerados.
O Box Plot, que estudamos no curso Green Belt, é uma ferramenta gráfica que ajuda a identificar a existência de possíveis outliers no conjunto de dados.
Em um boxplot são apresentadas 5 estatísticas: o mínimo, o primeiro quartil (Q1), a mediana, o terceiro quartil (Q3) e o máximo. Esses valores também são chamados de resumo dos cinco números.
Para construir um desenha-se um retângulo alinhado verticalmente (ou horizontalmente) com duas semirretas, uma em cada um dos lados opostos do retângulo.
A altura do retângulo é definida pelos quartis Q1 e Q3. Uma linha secciona o retângulo no valor da mediana (ou Q2). As semirretas ligam respectivamente os quartis Q1 e Q3 ao valor mínimo e ao máximo do conjunto de dados.
Confira no exemplo o Box Plot “desenhado” com as estatísticas do resumo de cinco pontos.
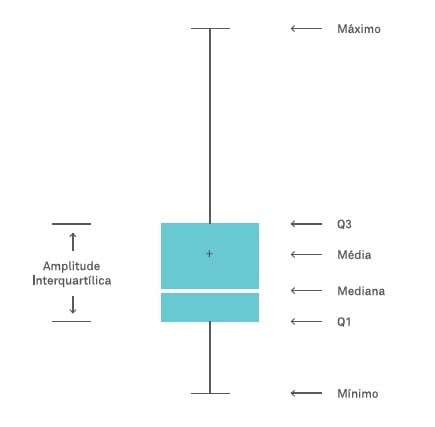
Figura: exemplo de box plot e as estatísticas por ele representadas.
Não existe uma única forma de apresentar um gráfico Box Plot. Diferentes livros (ou softwares) adotam variações na apresentação dos pontos extremos. O gráfico, em seguida, apresenta o Box Plot para o valor de venda de um produto amostrado em 95 pontos de venda.
Box Plot: Interpretação
O grande objetivo é verificar a distribuição dos dados. Assim, as conclusões que tiramos ao analisar um box plot são: centro dos dados (a média ou mediana), a amplitude dos dados (máximo – mínimo), a simetria ou assimetria do conjunto de dados e a presença de outliers.
Vamos detalhar essas interpretações:
O centro da distribuição é indicado pela linha da mediana, no centro do quadrado.
A dispersão é representada pela amplitude do gráfico, que pode ser calculada como máximo valor – mínimo valor. Quanto maior for a amplitude, maior a variação nos dados.
O retângulo contém 50% dos valores do conjunto de dados. A posição da linha mediana no retângulo informa sobre a assimetria da distribuição.
Uma distribuição simétrica teria a mediana no centro do retângulo. Se a mediana é próxima de Q1, então, os dados são positivamente assimétricos.
Se a mediana é próxima de Q3 os dados são negativamente assimétricos. No exemplo que você pode observar, a seguir, a distribuição dos dados é simétrica.
Os outliers em um box plot aparecem como pontos ou asteriscos fora das “linhas” desenhadas. Perceba que no exemplo que temos um outlier representado pelo ponto no começo do gráfico.
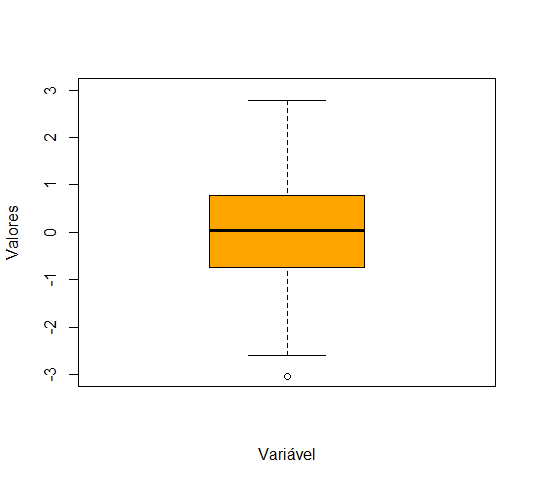
Figura: exemplo de box plot com outlier.
O que são os outliers em um Box plot
O comprimento das linhas fora do retângulo (algumas vezes chamadas de whisquers) informam sobre a cauda da distribuição.
Os outliers serão os valores fora de Q1-1.5*(Q3-Q1) e Q3+1.5*(Q3 -Q1).
Exemplo de exercício resolvido de box plot
Exemplo: Um engenheiro em uma indústria química é responsável pela produção de acetona. Para avaliar a linha de produção, o gerente monitora o processo.
Durante uma semana, 16 bateladas de acetona são produzidas e uma leitura por batelada é feita. Os resultados são apresentados na tabela abaixo.
|
Batelada |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Leitura |
6 |
24 |
12 |
11 |
34 |
32 |
28 |
19 |
31 |
22 |
29 |
58 |
15 |
5 |
17 |
25 |
Arrumamos os dados em ordem crescente:
5, 6, 11, 12, 15, 17, 19, 22, 24, 25, 28, 29, 31, 32, 34, 58
Desses dados calculamos os quartis, a mediana a distância entre quartis, o mínimo e o máximo:
Q1=13.5 M=23 Q3=30
IQR=16.5 Min=5 Max=58
O Box plot é apresentado a seguir.
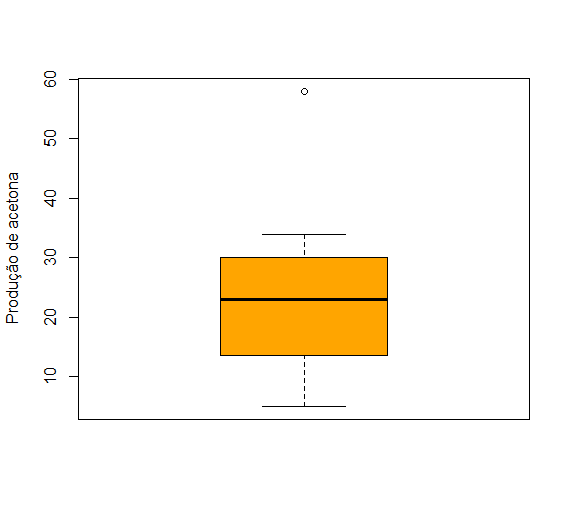
Figura: outro exemplo de box plot com outlier.
Boxplot comparativo ou estratificado
Além de fornecer informações importantes sobre um conjunto de dados, o Boxplot é usado para comparar graficamente mais de um conjunto de medidas com respeito à média, à dispersão e à distribuição.
Isso pode ser conseguido desenhando-se os Box Plots para cada conjunto de dados, paralelamente, num mesmo gráfico.
O próximo conjunto de dados apresenta dados de viscosidade de três misturas diferentes
| Mistura 1 | Mistura 2 | Mistura 3 |
| 22.02 | 21.49 | 20.33 |
| 23.83 | 22.67 | 21.67 |
| 26.67 | 24.62 | 24.67 |
| 25.38 | 24.18 | 22.45 |
| 25.49 | 22.78 | 22.29 |
| 23.50 | 22.56 | 21.95 |
| 25.90 | 24.46 | 20.49 |
| 24.89 | 23.79 | 21.81 |
O Box Plot comparativo é apresentado a seguir:
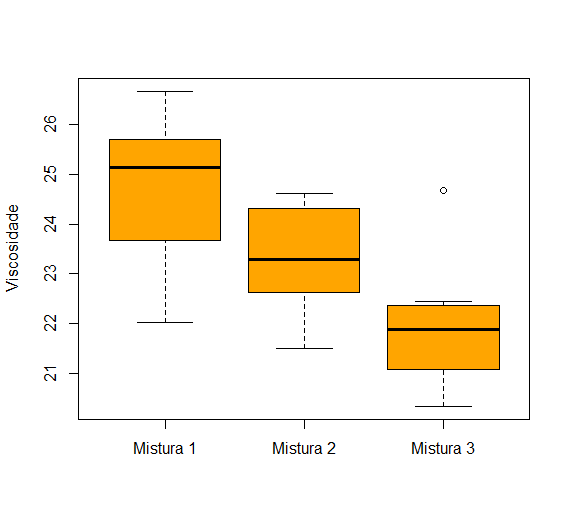
Figura: exemplo de box plot estratificado (comparativo).
Como podemos observar, as misturas apresentam níveis médios diferentes de viscosidade, decrescentes da mistura 1 para a mistura 3.
Como fazer um Box Plot com um software
Existem alguns programas de computador que permitem a construção de um Box Plot. Os principais são o Excel, o Minitab e o R. Confira na sequencia como preparar o gráfico em cada um desses softwares para facilitar suas análises.
Como fazer um Boxplot no excel
Para preparar um boxplot no excel você primeiro precisará calcular os seguintes valores: mínimo, Q1 (primeiro quartil); mediana; Q3 (terceiro quartil) e máximo.
Depois, basta utilizar a planilha que preparamos. É só inserir as informações e você fica com seu boxplot prontinho para ser apresentado.
Como construir um Box Plot no R
O R é um software livre muito utilizado pelos estatísticos. Ele permite a execução de análises mais sofisticas, mas exige um conhecimento de sua linguagem de programação.
Se você tiver com os dados no R, basta chamar a função boxplot(). Vamos supor que o conjunto de dados se chama DATA. Para preparar o gráfico Box Pot no R basta executar o comando boxplot(DATA).
Você pode utilizar qualquer um dos conjuntos de dados apresentados nesse material para treinar a execução no R.
Como construir um Boxplot no Minitab
O Minitab é um software estatística muito utilizado para a construção de gráfico e análise de dados devido a facilidade de aprendizado de suas ferramentas e na velocidade de preparação de gráficos.
Se quiser, você pode fazer o download gratuito de uma versão de teste do Minitab diretamente do site deles, basta procurar por “download minitab” em seu buscador favorito.
Se você tem um Minitab a disposição, vamos mostrar como construir um Boxplot. Você baixar os dados para esse exemplo no Excel no link exemplo-boxplot-minitab e copiar os dados (Crtl+C) e colar (Crtl+V) em seu Minitab que irá funcionar normalmente.
Com o Minitab abetos e os dados prontos para a análise siga o caminho Graph>>Boxplot.
Nesse momento se abrirá 4 opções para construção de Boxplot. As duas de cima são utilizadas quando a variável numérica esta em uma única coluna.
Por exemplo, se em uma coluna estivesse todos os dados viscosidade estivessem em uma coluna e em uma outra coluna a informação de a qual mistura os dados pertencem).
No nosso exemplo temos os dados de viscosidade em 3 colunas e é isso que o Minitab chama de “Multiple Y’s”. Como não existe outra variável de estratificação selecionamos “Multiple Y’s>Simple”.
Quando se abrir a janela de configuração do Boxplot você deve inserir as variáveis Mistura 1, Mistura 2 e Mistura 3 na opção “Graph variables” e apertar OK.
O gráfico Box plot será gerado instantaneamente. Preparamos 4 figuras com esses passos para ajudá-lo a construir o Boxplot no Minitab.
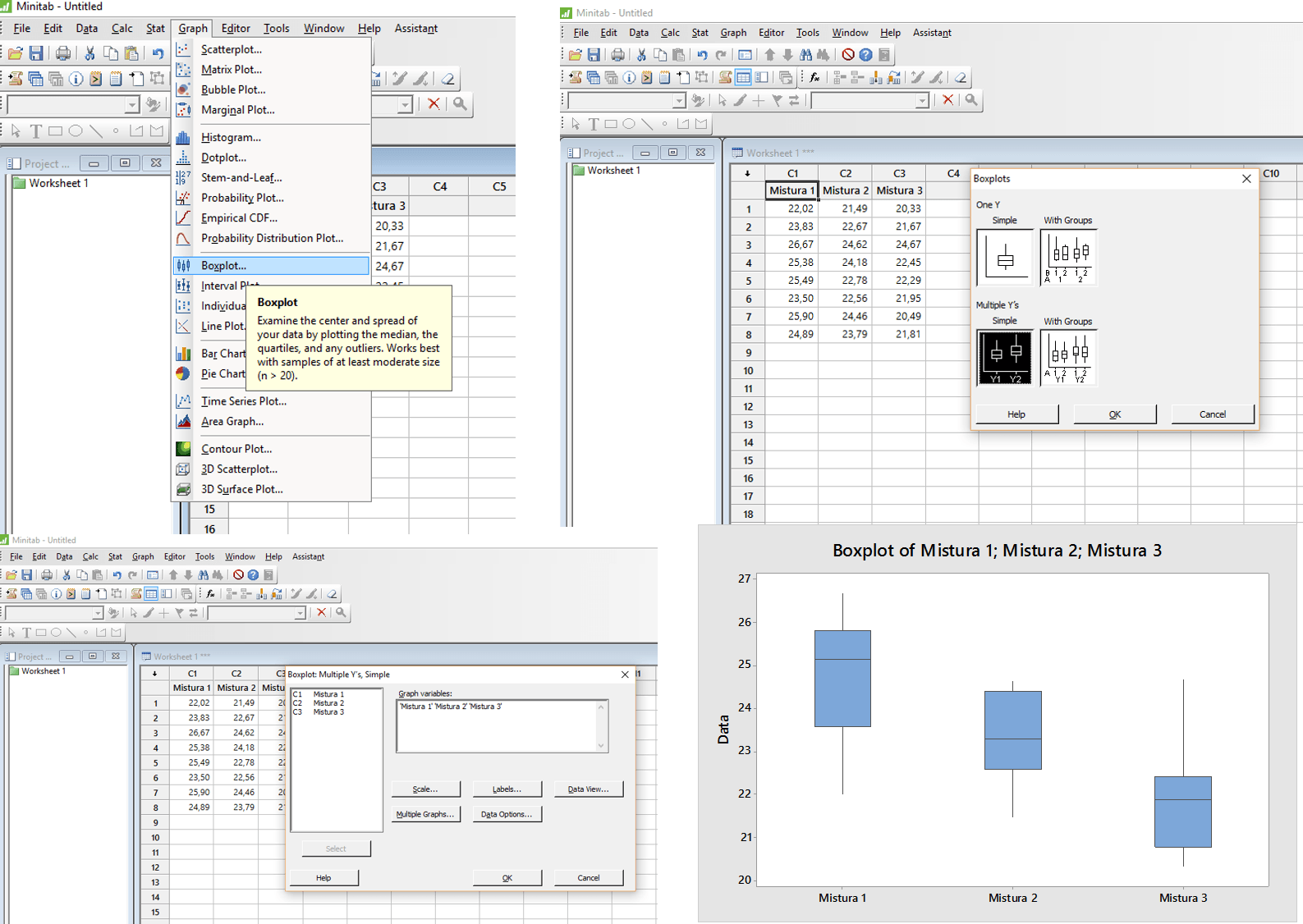
Figura: comandos para executar um box plot no Minitab.
Conclusão
Agora que você já sabe como utilizar, é muito importante saber quando utilizar o gráfico box plot. Quer se tornar um expert em Box Plot? Então, matricule-se no curso Green Belt, para dominar esse e outros conhecimentos para trabalhar com a metodologia Six Sigma que utiliza o 5W2H.
Você tem algum comentário adicional? Alguma aplicação interessante de Boxplot para comentar? Compartilhe conosco seus comentários!


porque é utilizado 1,5 para calcular os valores extremos?
Oi Márcio,
É um definição. Espera-se que se a distribuição for simétrica, dados fora desse limite sejam indicação de outliers.
Abraços
Acredito que o uso do 1,5 é por conta da normal.
Q3-Q1=0.6745×2=1,349… arredondado para 1,5
E apresentam 99,3% dos dados.
Li essa justificativa em um trabalho uma vez e achei plausível.
e quando não aparecer linha no meio do retangulo? fiz uma comparação em dois aparelhos usados e em apenas um “bloco” apareceu a linha de simetria. como devo interpretar
provavelmente é que a mediana coincidiu com o Q1 ou Q3
Q1 não seria 12 e Q3 31
Não Marcelo, como temos 16 observações o Q1 é um valor entre a quarta e quinta observação (geralmente utilizamos a média, nesse caso 13.5). A mesma lógica se aplica para o Q3.
ola
estou com dificuldades de interpretar os dados do box plot através do histograma. como faço?
Poderia me dar um exemplo
Obrigada