Uma aplicação muito interessante de experimentos fatoriais
Sempre que leciono sobre experimentos fatoriais, uma das farramentas mais importantes vistas nos cursos de Green Belt e Black Belt, me deparo com uma dificuldade: convencer os alunos que o p‐valor calculado pelos softwares estatísticos deve ser analisado com muito cuidado. Na realidade, eu os oriento a, em geral, ignorá‐los, principalmente em fatoriais de resolução III.
Minha sugestão é, no caso do MINITAB, por exemplo, trocar o nível de significância default de 0.05 para 0.99 para que a linha vermelha que aparece no gráfico de Pareto dos Efeitos correspondendo ao nível de significância escolhido fique encostada no eixo Y ou que o gráfico probabilístico Normal dos efeitos identifique todos os efeitos. Dessa forma, é responsabilidade do analista decidir o que fazer em seguida (o que considerar significante). Não é tarefa fácil, dada a prática disseminada de usar o nível de significância de 5% (ou 1% ou 10%) para decidir o que é significante.
Ao usar essa abordagem, podem se perder oportunidades fantásticas de aprendizado e de melhorar processos.
Box (1990) relata um experimento fatorial 23 realizado por Christer Hellstrand, ex‐aluno de pós‐graduação da University of Wisconsin. O objetivo inicial era realizar um experimento comparativo de dois projetos da gaiola de rolamento na produção de rolamentos. Os níveis eram o projeto atual e uma modificação que apresentava redução no custo de fabricação. A variável resposta era a durabilidade do rolamento.
A duração seria medida por meio de um teste acelerado.
O plano inicial dos engenheiros era produzir quatro rolamentos com a gaiola atual e quatro com gaiola modificada. Christer perguntou aos engenheiros se não haveria outros fatores que eles gostariam de testar. Eles disseram que sim, mas não havia recursos para a execução de corridas experimentais além das oito planejadas. Christer mostrou como usar o fatorial 23 para incluir dois fatores adicionais sem aumentar o custo do experimento. Os fatores adicionais foram tratamento térmico com dois níveis e o anel externo do rolamento com dois níveis.
O plano experimental proposto (na ordem canônica) com as respostas obtidas está na tabela 1 (os níveis estão codificados, sendo o nível (‐) o atual).
Tabela 1: Plano Experimental
| Anel Externo | Gaiola | Trat Term | Tempo de vida |
| ‐1 | ‐1 | ‐1 | 17 |
| 1 | ‐1 | ‐1 | 25 |
| ‐1 | 1 | ‐1 | 19 |
| 1 | 1 | ‐1 | 21 |
| ‐1 | ‐1 | 1 | 26 |
| 1 | ‐1 | 1 | 85 |
| ‐1 | 1 | 1 | 16 |
| 1 | 1 | 1 | 128 |
No MINITAB, o gráfico de Pareto dos efeitos obtido com nível de significância de 5% (default) está na figura 2 abaixo.
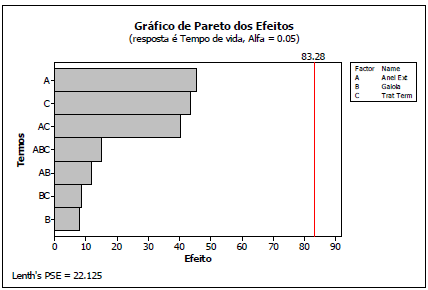
O ponto de corte (linha vermelha) correspondente ao nível de significância escolhido é calculado de acordo com proposta de Lenth (1989).
Ajustando o modelo com efeitos principais e interações de 2 fatores (usando o quadrado médio da interação dos três fatores como resíduo) obtêm‐se a seguinte tabela ANOVA:
Tabela ANOVA dos Efeitos
| Term | Effect | Coef | SE Coef | T | P |
| Constant | 42.125 | 7.375 | 5.71 | 0.110 | |
| Anel Ext | 45.250 | 22.625 | 7.375 | 3.07 | 0.201 |
| Gaiola | 7.750 | 3.875 | 7.375 | 0.53 | 0.692 |
| Trat Term | 43.250 | 21.625 | 7.375 | 2.93 | 0.209 |
| Anel Ext*Gaiola | 11.750 | 5.875 | 7.375 | 0.80 | 0.572 |
| Anel Ext*Trat Term | 40.250 | 20.125 | 7.375 | 2.73 | 0.224 |
| Gaiola*Trat Term | 8.750 | 4.375 | 7.375 | 0.59 | 0.659 |
Se o nível de significância de 5% (ou mesmo 10%) for utilizado para decidir sobre quais efeitos ou interações são significantes a conclusão é que nenhum efeito ou interação é significante, o que, se fosse verdade, seria um resultado útil, visto que abriria a possibilidade de usar o novo projeto de gaiola na fabricação com redução de custos.
O gráfico de Pareto dos efeitos com nível de significância de 0.99 está na figura a seguir. Os efeitos principais de A e C e a interação AC se destacam.
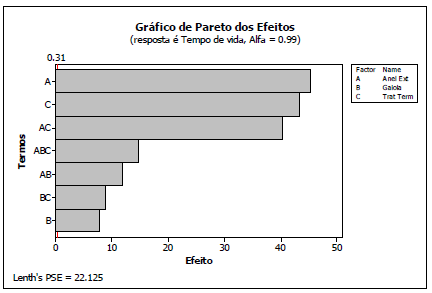
Um exame cuidadoso na tabela de dados mostra um resultado surpreendente. O tempo de vida nas novas condições (+,+,+) é 7.5 vezes maior que na condição original.
Ignorando o p‐valor como critério de decisão do que é significante e prosseguindo na análise com os três maiores efeitos (A. C e AC), o gráfico da interação entre A e C (figura 4) mostra exatamente o que se pode deduzir da própria tabela. A combinação dos níveis (+) de A (Anel Externo) e (+) de C (Tratamento Térmico) são responsáveis pelo aumento no tempo de vida. O fator de interesse inicial (Cage) não tem impacto relevante no tempo de vida, o que nesse caso é um bom resultado, visto que a nova condição reduz custo sem impactar negativamente no tempo de vida.
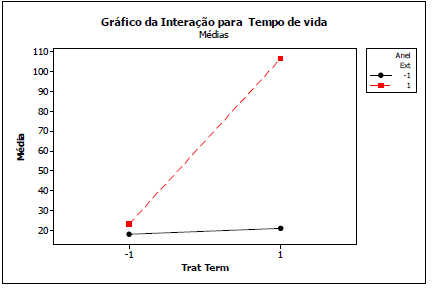
Nessas situações é importante testar a “receita” proposta pelo experimento para verificar se os resultados obtidos se confirmam. No caso em particular, a “receita” foi implementada com substancial redução de custo e melhoria na qualidade (duração).
Alguns aprendizados importantes desse experimento:
1) Experimentos fatoriais 2n (em particular 23) são relativamente simples de analisar;
2) Não é necessário usar ANOVA, p‐valor, relação sinal ruído ou qualquer outro tipo de técnica para analisar o experimento.
3) Como mostra o exemplo apresentado, o uso do p‐valor como critério de decisão pode ser contraproducente e induzir o experimentador a perder oportunidades de aprendizado e melhoria.
Nesse exemplo vimos uma aplicação prática da técnca de experimentos fatoriais. Se você gostou da maneira descomplicada pela qual apresentamos conceitos estatísticos importantes, consulte nossos cursos.
Se tiverem qualquer dúvida, por favor escrevam para [email protected]. Será um prazer ajudá-los!
Muito bom!
Obrigado Danilo!
Vamos tentar convencer o prof Ademir a escrever mais textos desse tipo.
abraços,
Ótimo material, a coletânea DOE
Prof Marcelo
Obrigado por disponibilizar seus materiais; todos ótimos
e claros suas explicações.
Abçs
Sérgio