No post de hoje iremos falar sobre o gráfico de CUSUM, que incorporam todas as informações na sequência de valores de amostras e auxilia nos projetos de melhoria. Continue acompanhando para saber mais!
eBook: Como fazer análise de dados
A análise de dados tem sido uma habilidade cada vez mais requisitada no mercado de trabalho. A quantidade de dados disponíveis é enorme, mas poucas pessoas conseguem transformá-los em insights para decisões de negócios.
Os gráficos de Shewhart são de simples interpretação e muito úteis nos nossos projetos de melhoria, principalmente no início de um processo, em que é muito provável que existam falhas ocasionais ou haja grande variação.
Uma desvantagem dos gráficos de Shewhart é que esses gráficos ignoram qualquer informação dada pela sequência de pontos anterior, ou seja, não possuem memória.
Essa característica torna esses gráficos insensíveis a pequenas mudanças nos processos. Assim, após terminada a primeira fase do projeto, onde estabilizamos o processo e reduzimos a variação, é provável entrarmos em uma etapa onde haja dificuldade para identificarmos mudanças, já que as variações podem não ser amplas o suficiente para serem detectadas nos gráficos de controles usuais.
Um aprimoramento do gráfico X de Shewhart e uma solução para esse problema é a utilização do gráfico de controle de soma cumulativa (CUSUM) que incorporam todas as informações na sequência de valores da amostra, sendo mais sensíveis na detecção de pequenas variações e mais apropriado para reconhecer o histórico dos dados.
Para plotar o gráfico de CUSUM começamos procurando desvios em relação à média, ou seja, a diferença entre o valor observado e um valor alvo (média histórica do processo ou média ideal do processo).
Com o cálculo desses desvios podemos identificar qualquer deslocamento na média do processo, mesmo com pequenas variações. Nesses gráficos, um processo está sob controle se a soma cumulativa desses desvios oscila em torno de 0.
Caso a média do processo seja deslocada, será possível identificar uma tendência (positiva ou negativa) no gráfico, confirmando essa mudança.
Planejando o Gráfico de CUSUM
O planejamento do CUSUM visa fornecer um bom desempenho do comprimento médio da sequência (CMS), que indica a média de pontos necessários para a ocorrência de um ponto fora dos limites de controle. O comprimento médio da sequência é impactado diretamente pela escolha dos parâmetros k e h.
O parâmetro k está relacionado com a magnitude da mudança que queremos identificar, enquanto que o parâmetro h indica o intervalo de confiança para detecção de causas especiais.
A escolha dos parâmetros k e h, deve ser realizada de modo que sua seleção fornece bom desempenho para o número médio de amostras necessárias até o alarme.
Montgomery (2009), traz em seu livro, Introduction to statistical quality control, a tabela de Comprimento Médio da Sequência.
Essa tabela auxilia na verificação da quantidade média de pontos necessários para identificar uma mudança de acordo com a magnitude sigma. Ele também apresenta como calcular este comprimento com diferentes valores de parâmetros.
Quando queremos identificar mudanças de cerca de 1,5 desvio padrão da média do processo tem-se obtido bons resultados com k = ½ e h = 4 ou 5.
Com esses valores de parâmetros teremos um CMS de 10 pontos, ou seja, o gráfico de CUSUM nos traz um sinal de causa especial, a cada 10 amostras, se houver um deslocamento da média em relação ao alvo. O valor de k amplamente utilizado na prática é de 0,5, que significa que estamos ignorando variações de meio desvio padrão no processo.
Exemplo: Analisando o Gráfico de CUSUM
Um laboratório que realiza exames de sangue possui um rigoroso controle de qualidade com amostras de valores conhecidos (soro controle) referenciados por uma empresa certificada.
Para garantir o correto diagnóstico dos pacientes, diariamente é realizado o teste de soro controle e os valores obtidos são acompanhados em uma planilha e nos gráficos de controle.
Para ilustrar vamos pegar o exemplo do exame de TSH, onde temos como média histórica reconhecida da concentração de TSH (variável resposta) do soro controle o valor de 10 uUI/ml com desvio padrão de 1 uUI/ml.
Os resultados obtidos da análise do soro controle pertencem a uma população normal. Analisando os dados pelo gráfico de Shewhart temos:
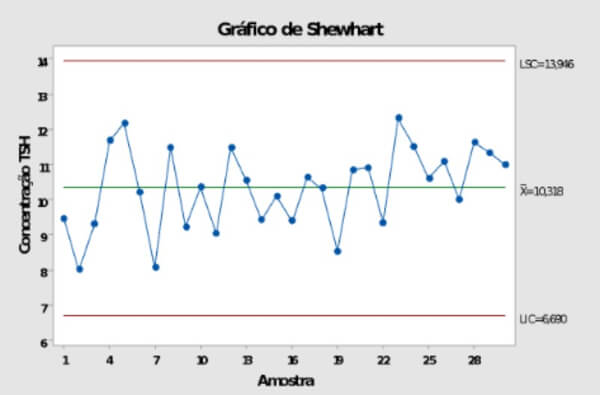
Nesse gráfico não encontramos nenhuma evidência de causa especial , ou seja, que requer uma ação local.
Saiba mais: Falhas ocasionais que ocorrem durante o processo não sendo parte de sua variabilidade natural. Acesse o link.
Relembrando que algumas das regras propostas por Shewhart para detecção de causas especiais são: 8 pontos consecutivos abaixo ou acima da média; 6 pontos consecutivos crescentes ou decrescentes e pontos foras dos limites de especificação.
Como estamos interessados em identificar uma mudança de magnitude em torno de 1 desvio padrão, vamos utilizar o CUSUM tabular para analisar os dados. Assim vamos definir nosso k=12 e h = 5.
O gráfico do CUSUM é constituído de duas linhas – CUSUM unilateral superior (linha com pontos azuis) e CUSUM unilateral inferior (linha com pontos brancos).
Vamos calcular os dados para a 1ª amostra, ou seja, os primeiros pontos plotados de cada linha. O primeiro passo é calcular os desvios.
O valor observado da amostra foi 9,45. Para a linha com pontos azuis subtraímos (alvo + k = 10,5) do valor da amostra (9,45), temos então um desvio de -1,05, que precisa ser somado ao valor do ponto anterior. Como ainda estamos no primeiro ponto utilizamos o valor inicial de 0. Logo o valor o primeiro ponto será o máximo entre 0 e -1,05.
Para a linha com pontos brancos, a primeira amostra é subtraída do valor (alvo – k = 9,5), que nos dá um valor de 0,05. Também temos o valor inicial de 0, logo o primeiro ponto será o máximo entre 0 e 0,05.
Agora vamos calcular os valores para a segunda amostra, cujo valor foi de 7,99.
A diferença entre 7,99 e 10,5 é -2,51. Calculado o desvio temos que somá-lo ao ponto anterior do gráfico que é zero. Logo o segundo ponto da linha com pontos azuis será o máximo entre -2,51 e 0.
A diferença entre 9,5 e 7,99 é 1,51. Somando o valor anterior de 0,05 temos que o segundo ponto será o máximo entre 1,56 e zero. Ou seja, estamos utilizando, em cada um dos pontos, a seguinte forma
Ci+=máx[0;Xi–(μ0+k)+Ci-1+]
Ci–=máx[0;(μ0-k)–Xi+Ci-1–]
em que o Ci+ é o valor do ponto na linha com pontos azuis (CUSUM unilateral superior) e Ci– é o valor do ponto na linha com pontos brancos (CUSUM unilateral inferior) Xi o valor da amostra e μ0 o valor alvo.
Continuamos os cálculos das amostras seguintes da mesma maneira, como pode ser observado na tabela a seguir.
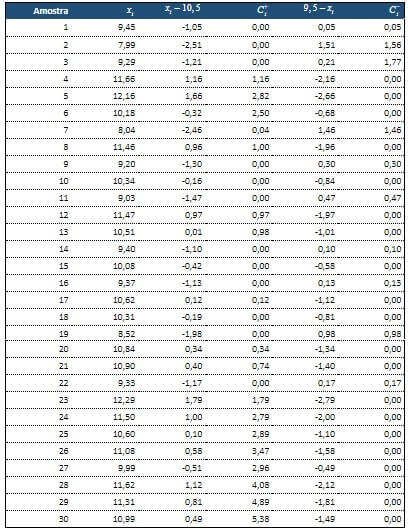
Com esta tabela, construímos o seguinte gráfico:
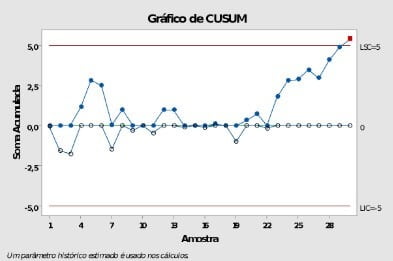
O gráfico é composto por duas linhas o CUSUM unilateral superior e CUSUM unilateral inferior. Através da análise desse gráfico podemos ver a plotagem dos CUSUMs, que são gerados a partir da soma acumulada dos desvios das amostras em relação à média do processo.
A partir do momento que o processo atinge um novo patamar, ponto 23, passamos a ter apenas desvios positivos, de modo que eles começam a se acumular resultando em um ponto fora dos limites de controle estatístico no ponto 30.
Isto indica que a média do processo sofreu alteração em relação à média alvo, sinal que não foi visto no gráfico de Shewhart, pois esses gráficos tem uma resposta mais lenta para pequenas variações na média.
Essa é uma das várias forma de monitorar processos. Continue aprendendo e se torne um expert em projetos de melhoria. Faça agora nosso curso de Black Belt acessando aqui!