Como havíamos falado em nosso post anterior (que você pode conferir acessando acessando o link a seguir: Conheça as principais ferramentas da qualidade).
Daremos continuidade aos posts dedicados as ferramentas de qualidade.
Através desses conteúdos pretendemos resgatar a importância e relevância dessas ferramentas para a evolução das empresas. No post de hoje iremos falar sobre o Gráfico de Distribuição!
Nova Apostila White Belt
Apostila totalmente gratuita para nossos alunos obterem uma experiência ainda melhor enquanto fazem o curso de Lean Six Sigma White Belt; ela conta com ilustrações próprias, identidade visual da escola e nova diagramação para melhor compreensão do conteúdo pelo aluno!
As sete ferramentas da Qualidade
As sete ferramentas da qualidade são um instrumento com capacidade demonstrada e reconhecido para reduzir custos e melhorar a qualidade de qualquer tipo de organização ou processo. Elas compreendem o conceito de identificação, entendimento e eliminação dos problemas. São elas:
- Distribuição (histograma e dot-plot);
- Gráfico de Pareto;
- Gráfico de dispersão;
- Diagrama de causa e efeito;
- Estratificação;
- Folha de verificação;
- Gráfico de controle
Distribuição (histograma e dot-plot)
Quando queremos colocar um prego na parede utilizamos um martelo. Da mesma forma, dependendo do tipo de variável que coletamos iremos utilizar uma ferramenta diferente. Os dados de um indicador podem ser:
Classificação (qualitativos)
Os resultados possíveis são classificações. No contexto de indicadores aparecerão na forma sim ou não (peça defeituosa ou não defeituosa, entrega atrasada ou não atrasada, cliente satisfeito ou não
satisfeito).
Contagem
Os resultados são números inteiros (número de riscos em uma peça, número de acidentes no mês).
Contínuos
Os resultados podem ser quaisquer números dentro de um intervalo (peso, comprimento, gasto mensal).
Depois de coletar os dados, a primeira atividade será resumi-los, uma vez que nosso cérebro não é preparado para compreender um extenso conjunto de dados.
Uma das maneiras mais simples de sumarizar os dados é o histograma. Para construir um histograma dividimos a amplitude dos dados em intervalos, preferencialmente de tamanhos iguais, e contamos o número de observações que estão em cada um dos intervalos.
A escolha desses intervalos é crítica, mas qualquer software que seja capaz de produzir um histograma possuí algoritmos que fazem esse cálculo de tal maneira a permitir a melhor visualização possível dos dados.
Para estudar o comportamento das vendas, um administrador coleta informações sobre o número de itens vendidos nos últimos 30 dias e constrói um histograma com o auxílio de um software.
Com esse gráfico ele percebeu que suas vendas variavam entre 28 e 52 unidades, e na maioria dos dias ele vendia em torno de 40.
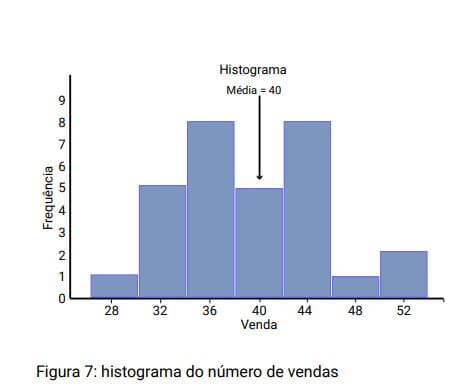
Outra maneira de enxergar a distribuição dos dados é o dot-plot, onde cada ponto no gráfico representa uma observação.

A média é uma estatística que resume uma informação muito importante da distribuição dos dados que é a centralidade.
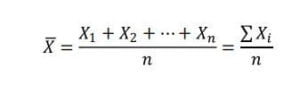
A média é denotada por X̅ e é calculada por onde os n valores retirados do processo são representados por X1,…,Xn.
Apesar de extremamente importante, a média não mostra todas as características do nosso processo.
Um fabricante de molas para sistemas de amortecimento precisa que seus produtos tenham comprimento de 45, com tolerância entre 42 e 48 cm.
Para verificar se estão atendendo a essa especificação o engenheiro responsável retira 50 peças de cada um das 2 linhas de produção e calcula as respectivas médias:

Ele anota esses dados e os envia para seu cliente, confiante de que seu processo era capaz de atender às especificações. Depois de uma semana ele recebe um e-mail de seu cliente solicitando providências para a linha 2,
que estava produzindo muitas peças fora da especificação.
Junto ao e-mail ele recebe os dot-plots das linhas 1 e 2.
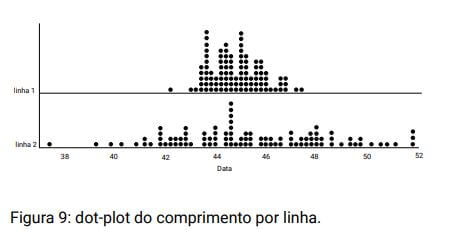
Olhando para os gráficos ele percebe, para sua surpresa, que realmente a linha dois estava produzindo muitas peças fora da especificação.
Nosso amigo acabara de aprender que não basta saber a média de um processo, precisamos também saber a respeito de sua variação, pois quanto menor a variação maior a qualidade do nosso processo.
Uma forma simples de medirmos a variação é pela soma de quão distante cada ponto está do centro (média):
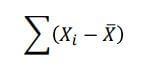
O problema é que essa soma é sempre 0. Por exemplo, no conjunto de dados 0, 1 e 2 a média é 1 e a soma dos desvios é:
![]()
Para resolver esse problema elevamos cada desvio ao quadrado, o que elimina os sinais negativos:
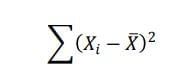
e para finalizar calculamos o desvio médio: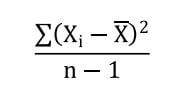
A razão de dividirmos por n-1 ao invés de n foge do escopo desse livro, mas a ideia por de traz continua sendo calcular a média das distâncias. Para voltarmos a escala original basta calcular a raiz quadrada desse valor:
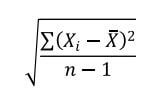
e essa estatística é chamada de desvio padrão e representada pela letra S. Aplicando esse cálculo às linhas de produção de rodas obteríamos o seguinte resultado:
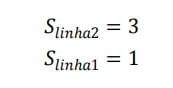
e nosso engenheiro perceberia que a linha dois produz muito mais peças não conforme do que a linha 1.
Amanhã daremos continuidade a nossa série falando sobre o Gráfico de Pareto. Continue acompanhando!
Lembrando sempre que nosso curso de Green Belt aborda essas ferramentas de forma aprofundada e o torna apto a aplica-las nos projetos de melhoria. Inscreva-se agora clicando aqui.
Pingback: Conheça as principais ferramentas da qualidade: Folha de verificação | Escola EDTI - Acesse e Conheça nossos Cursos
Pingback: Consultoria em estoque: quando e como contratar?