Os gráficos de controle são indispensáveis para entender a variação de um indicador ao longo do tempo, afinal, o controle de qualidade depende de ferramentas visuais.
Com elas, é possível estabelecer relações de causa e efeito e, a partir disso, definir ações corretivas e de melhoria.
Acompanhe neste texto alguns exemplos e saiba em que tipo de ações e projetos os gráficos de controle podem ser aplicados!
O que são gráficos de controle?
Gráficos de controle são instrumentos usados para medir a intensidade de um desvio e para saber se um determinado padrão está sendo seguido, entre outros usos.
Na metodologia Lean Six Sigma, eles são frequentemente acionados para aferir o quanto um certo parâmetro está se afastando do padrão e até para saber qual é o parâmetro ideal.
Como veremos mais à frente, estas ferramentas dão uma noção precisa a respeito de um problema, permitindo assim que possam ser tomadas as medidas de controle necessárias.
Para que servem os gráficos de controle?
A função principal de um gráfico de controle é orientar a respeito do andamento de um processo.
Imagine que, em uma indústria de autopeças, seus gestores querem saber se um lote está com as medidas dentro do padrão considerado normal para poder enviá-las para venda.
Para isso, eles precisarão medi-las, gerando assim um volume de dados considerável sobre cada unidade.
Um gráfico de controle, nesse caso, será a “régua” usada para saber se essas medidas correspondem aos padrões de qualidade previamente estabelecidos.
Exemplos de gráficos de controle
Melhor do que falar sobre os gráficos é entendê-los com exemplos práticos extraídos de casos reais.
Você vai notar que, em cada um deles, há um problema concreto a ser solucionado e uma relação de causa e efeito a ser estudada.
Procuramos traduzir os termos mais técnicos da forma mais simples possível para destacar o que estava em jogo em cada uma dessas análises.
Acompanhe!
Gráfico de controle de gastos
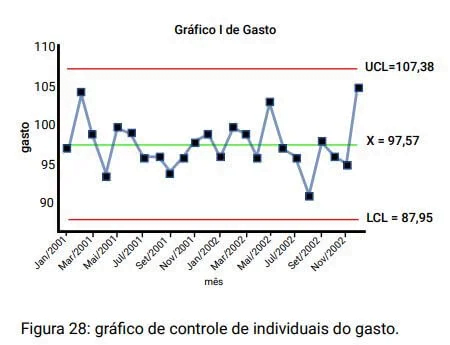
Os limites de controle neste gráfico são estabelecidos de tal forma que mais de 99% dos dados fiquem entre eles.
Assim, se um ponto cai além desses limites, temos uma chance menor do que 1% de ser uma causa comum e, portanto, existe forte evidência de uma causa atípica.
Esse critério foi definido por Walter Shewhart, o criador da ferramenta, que pode ser conhecida em detalhes no livro “Introduction to Statistical Quality Control”, de Douglas Montgomery.
O gráfico acima mostra uma aplicação desse gráfico, usado para fazer o monitoramento do gasto mensal com treinamento.
Cada ponto no gráfico representa o gasto de um mês e, nesse caso, dizemos que o subgrupo é de tamanho 1 (um mês).
Além disso, estamos trabalhando com uma variável contínua (gasto com treinamento), o que implica utilizar o gráfico de individuais.
Gráfico Barra x Diâmetro
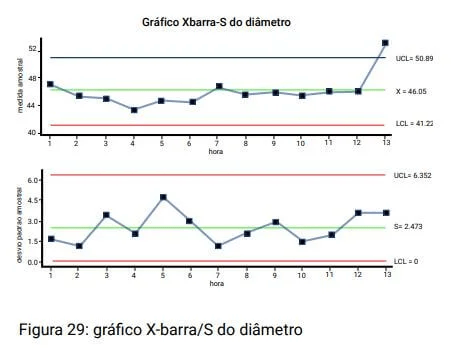
Em certas linhas de montagem, é comum a retirada de algumas peças ao final de uma hora de produção para avaliar a qualidade e realizar ajustes nas máquinas quando necessário.
No gráfico acima, temos o exemplo de uma empresa de autopeças que retirava 5 rodas por hora, uma de cada uma de suas 5 linhas de produção, para medir os respectivos diâmetros.
Dessas cinco peças, era possível calcular o diâmetro médio e o desvio padrão para monitoramento estatístico ao longo do tempo.
Chamamos o gráfico produzido com a média de X-barra (X) e o gráfico produzido com o desvio padrão de S, de Standard Deviation, o desvio padrão.
Na hora 13, aparece a indicação de uma causa especial no gráfico X-barra, mas não no gráfico S, indicando que a média do diâmetro das peças mudou, mas não a variação entre elas.
Com essa informação, podemos concluir que temos uma causa especial que afetou todas as peças, causando um aumento de diâmetro em todas elas.
Essa indicação levou a descobrir que um lote de matéria-prima que estava abastecendo todas as cinco linhas apresentava problemas.
Gráfico de defeitos por metro quadrado
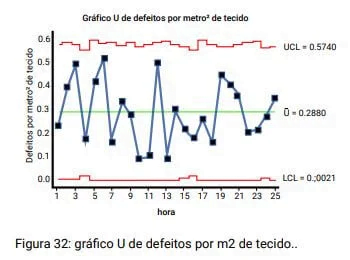
O gráfico acima foi extraído de uma grande empresa de tecelagem, que monitorava o número de defeitos por rolo de tecido produzido, com os rolos variando de tamanho.
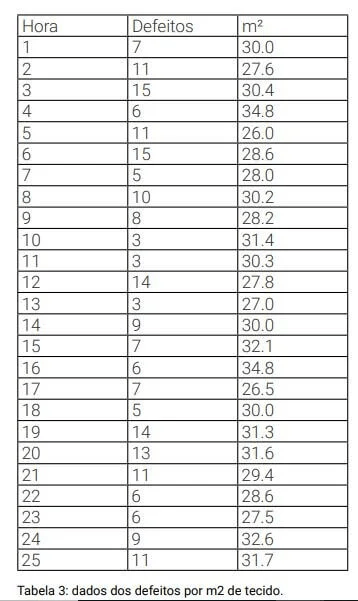
A cada hora, era retirado um rolo e anotava-se o número de defeitos e a área (em m2) de tecido.
A Tabela 3 apresenta o número de defeitos e o tamanho, em metros quadrados, dos rolos produzidos.
Monitorou-se, nesse caso, o número de defeitos por cm², já que os tamanhos dos rolos eram diferentes entre si.
Assim, os limites de controle eram diferentes para cada ponto.
Uma vez que o subgrupo (nesse caso o tamanho do rolo) é um componente do cálculo, foi preciso estabelecer uma unidade de medida comum que, no caso, seria por centímetros.
Como aprender sobre gráficos de controle?
A partir do que vimos, os gráficos de controle só podem ser construídos adequadamente por profissionais capacitados.
Para isso, a Escola EDTI forma especialistas na metodologia Lean Six Sigma há mais de uma década, qualificando-os para solucionar os problemas das empresas.
Chegou a sua vez de se tornar um verdadeiro mestre nos gráficos de controle e ferramentas de qualidade.
Conheça os cursos presenciais e EAD da EDTI e dê um salto na sua carreira.
Seja o profissional que as empresas querem ter, com uma formação reconhecida pela The Council for Six Sigma Certification (CSSC).
Seja qual for o seu desafio profissional, a EDTI ajuda você a superá-lo!
Conclusão
Gráficos de controle estão entre as ferramentas mais utilizadas em projetos na metodologia Lean Six Sigma.
Saber como construí-los é essencial para liderar equipes responsáveis por ações de melhoria, bem como de controle de qualidade.
Para isso, como vimos neste texto, é necessária uma formação direcionada, que oferecemos nos cursos Green Belt e Black Belt da EDTI.
Pingback: Governança de projetos: benefícios e como implementar